Коинфлипы
Предположим, что вы подбрасываете монетку 100 раз, по итогам получая 60 “орлов” и 40 “решек”, что довольно существенно отличается от ожидаемого распределения: 50-50. Почему распределение результатов произошло именно таким образом?
Для ответа на этот вопрос нам следует воспользоваться биноминальным калькулятором, задав для расчета следующие переменные:
- вероятность выпадения орла, которая равна 0,5 или 50%.
- количество попыток, равное 100.
- полученный результат, который вы хотите проверить (в нашем случае 60 орлов).
Посчитав, калькулятор покажет нам вероятность того, что на 100 бросков 60 раз выпадет именно “орел”: 0,0108 или чуть более 1%.
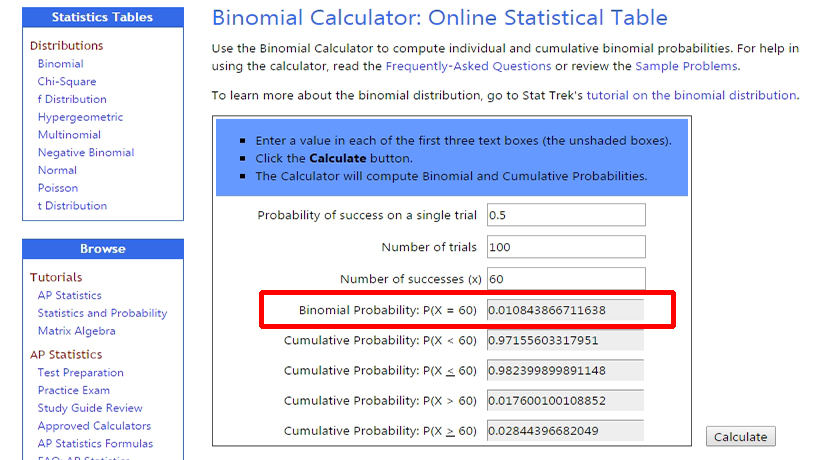
Также нас интересует нижняя строка, показывающая вероятность того, что на 100 бросков мы получим именно такое отклонение результата, то есть 60 и более “орлов”. Она равна: 0,028 или 2,8%. Говоря иначе, если сложить вероятности выпадения “60 орлов”, “61 орла”, “62 орлов” и так далее, то общая вероятность выпадения “больше 60 орлов” на 100 подбрасываний монеты будет равна почти 3%.
Перейдем к решению покерных задач посредством данного калькулятора.
Тузы
Допустим, вы играете в оффлайне, получая 30 рук в час. Какова вероятность того, что за четырехчасовую сессию или за 120 рук вы получите карманных тузов три раза?
Для начала вспомним вероятность получения карманных тузов: вероятность того, что первой картой у нас на руках окажется туз составляет 4/52 или 1/13. После этого в колоде останется 51 карта, три из которых – тузы, поэтому вероятность получения второго туза составит 3/51 или 1/17. Далее, перемножаем эти вероятности и получаем: 1/221 или 0,45%.
В биноминальный калькулятор забиваем – 0,0045. Количество испытаний – 120, и полученный результат – 3. Калькулятор говорит нам, что вероятность того, что за 120 рук нам три раза сдадут карманных тузов составляет 0,015 или 1,5%. Вероятность того, что нам сдадут тузов три и более раз за 120 рук немногим выше, а именно 1,7%.
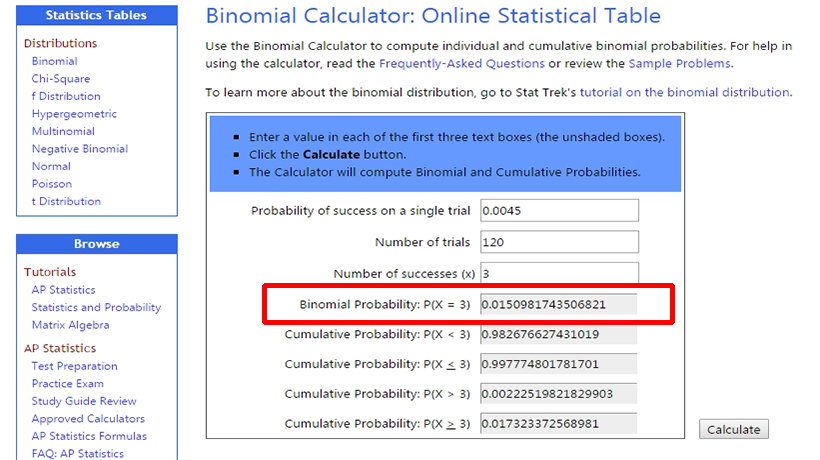
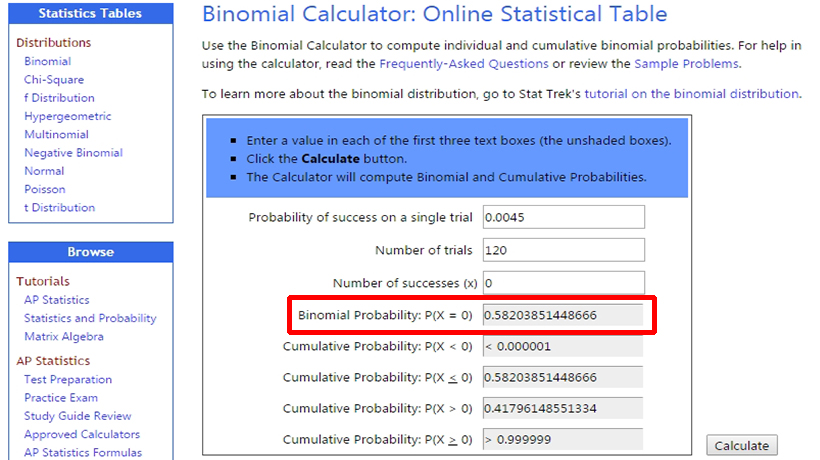
Теперь разберем обратную ситуацию, когда вам за сессию вообще не заходят тузы. Возьмем то же количество рук, ту же вероятность выхода тузов в одной руке и 0 в качестве полученного результата. Как часто нам будет так не везти? Калькулятор выдает нам вероятность 0,58 или 58%. Говоря иначе, более половины сессий продолжительностью в 120 рук будут проходить без карманных тузов.
Высокие карманные пары
Предположим, что наряду с тремя заходами карманных тузов, нам два раза сдают карманных дам и один раз карманных королей, то есть за сессию в 120 рук мы получаем шесть премиум стартеров.
Если рассчитывать каждую карманную пару отдельно, то вероятность будет та же, что и вероятность выхода тузов – 1/221. Таким образом, суммарная вероятность выхода тузов, королей или дам в любой руке составляет 3/221. В десятичной форме это 0,0136.
Забиваем в калькулятор полученный результат, равный 6, на 120 испытаний, и видим, что шанс получить за сессию в 120 рук шесть старших карманных пар составляет 0,004 или около 0,4%. Но больше всего нас интересует вероятность такой удачи, как минимум. Мы смотрим в нижнюю строку “X ≥ 6” и видим 0,006, или 0,6%.
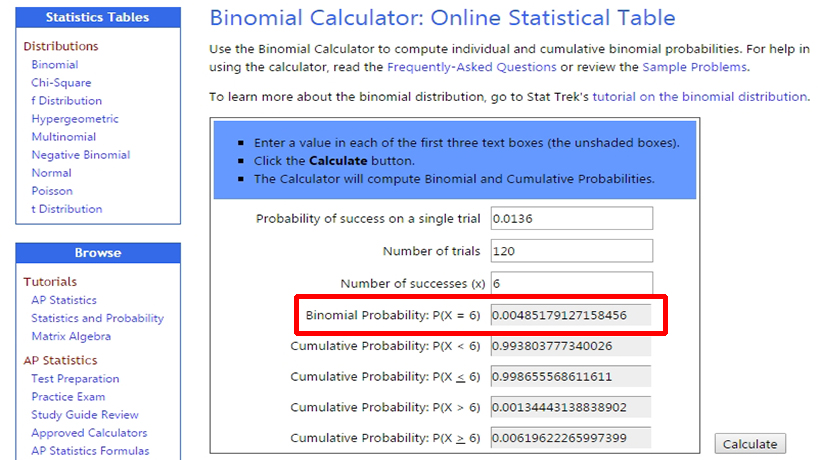
Выходит, что только около шести раз за тысячу сессий в 120 рук мы можем рассчитывать на апстрик, заключающийся в получении шести и более старших карманных пар.
Даунстрики
Предположим, что в какой-то из месяцев вы отыграли 30 сессий, из которых лишь 10 были выигрышными. Теперь вы желаете знать, насколько часто такое может происходить с вами в будущем.
Для ответа на этот вопрос нам необходимо знать вашу индивидуальную вероятность выигрышной или проигрышной сессии. Для этого обращаемся к HM2 или PT4 и видим, что, например, за несколько лет у вас было 65% выигрышных сессий и 35% проигрышных.
Таким образом, задача биномиального калькулятора определить вероятность получения только 10 выигрышей за 30 испытаний, когда вероятность выигрыша составляет 0,65.
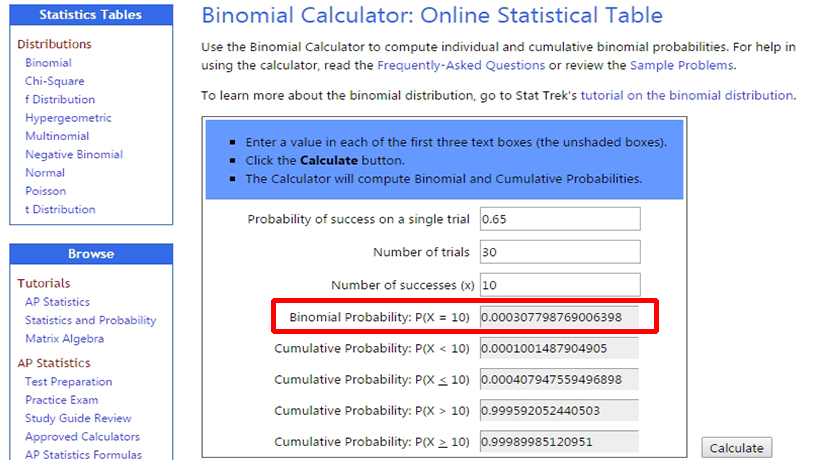
Итак, вероятность такого исхода составляет всего 0,0003 или 0,03%. Играя в покер на регулярной основе, вы можете предположить, что 20 минусовых сессий из 30 – не является чем-то из ряда вон выходящим. Вы будете совершенно правы, так как такое развитие событий не редкость в реальной жизни, как минимум, не 0,03%, как говорит нам математика, так что же происходит на самом деле?
Дело в том, что в предыдущих примерах мы работали с точными “статичными” переменными, в то время как вероятности выигрышной и проигрышной сессий зависят не только от математики, но и от таких факторов как ваш уровень игры, навыки ваших оппонентов, продолжительность сессии, ваше состояние и так далее, однако, с точки зрения калькулятора – вы робот.
Иногда вероятность получается настолько небольшой, что самым адекватным умозаключением будет не то, что вы просто испытали маловероятное событие, а то, что монетка на самом деле не настолько справедлива, как вам казалось. Таким же образом, объясняя большое количество проигрышных сессий, логически будет предположить, что в вашем небывалом даунстрике виновата не только дисперсия.
Биноминальный калькулятор говорит вам, что с вашим винрейтом случилось что-то далеко не случайное, и вам нужно понять, что это было, и как вы можете это исправить. Говоря иначе, виноватых в первую очередь следует искать в зеркале, а не где-то на стороне.




















